刘徽:中国古典数学理论的奠基人之一
2019-3-6 青野云麓
刘徽(约225年—约295年),汉族,山东滨州邹平市人,魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。刘徽思想敏捷,方法灵活,既提倡推理又主张直观。他是中国最早明确主张用逻辑推理的方式来论证数学命题的人。刘徽的一生是为数学刻苦探求的一生。他虽然地位低下,但人格高尚。他不是沽名钓誉的庸人,而是学而不厌的伟人,他给我们中华民族留下了宝贵的财富。

《九章算术》约成书于东汉之初,共有246个问题的解法。在许多方面:如解联立方程,分数四则运算,正负数运算,几何图形的体积面积计算等,都属于世界先进之列。刘徽在曹魏景初四年注《九章算术注》。
但因解法比较原始,缺乏必要的证明,刘徽则对此均作了补充证明。在这些证明中,显示了他在众多方面的创造性贡献。他是世界上最早提出十进小数概念的人,并用十进小数来表示无理数的立方根。在代数方面,他正确地提出了正负数的概念及其加减运算的法则,改进了线性方程组的解法。在几何方面,提出了'割圆术',即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法。他利用割圆术科学地求出了圆周率π=3.1416的结果。他用割圆术,从直径为2尺的圆内接正六边形开始割圆,依次得正12边形、正24边形……,割得越细,正多边形面积和圆面积之差越小,用他的原话说是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”他计算了3072边形面积并验证了这个值。刘徽提出的计算圆周率的科学方法,奠定了此后千余年来中国圆周率计算在世界上的领先地位。

刘徽在数学上的贡献极多,在开方不尽的问题中提出“求徽数”的思想,这方法与后来求无理根的近似值的方法一致,它不仅是圆周率精确计算的必要条件,而且促进了十进小数的产生;在线性方程组解法中,他创造了比直除法更简便的互乘相消法,与现今解法基本一致;并在中国数学史上第一次提出了“不定方程问题”;他还建立了等差级数前n项和公式;提出并定义了许多数学概念:如幂(面积);方程(线性方程组);正负数等等.刘徽还提出了许多公认正确的判断作为证明的前提.他的大多数推理、证明都合乎逻辑,十分严谨,从而把《九章算术》及他自己提出的解法、公式建立在必然性的基础之上。虽然刘徽没有写出自成体系的著作,但他注《九章算术》所运用的数学知识,实际上已经形成了一个独具特色、包括概念和判断、并以数学证明为其联系纽带的理论体系。
刘徽在割圆术中提出的'割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣',这可视为中国古代极限观念的佳作。《海岛算经》一书中,刘徽精心选编了九个测量问题,这些题目的创造性、复杂性和富有代表性,都在当时为西方所瞩目。刘徽思想敏捷,方法灵活,既提倡推理又主张直观。他是我国最早明确主张用逻辑推理的方式来论证数学命题的人。

代表著作
著作简介
其代表作《九章算术注》是对《九章算术》一书的注解。《九章算术》是中国流传至今最古老的数学专著之一,它成书于西汉时期。这部书的完成经过了一段历史过程,书中所收集的各种数学问题,有些是秦以前流传的问题,长期以来经过多人删补、修订,最后由西汉时期的数学家整理完成。现今流传的定本的内容在东汉之前已经形成。《九章算术》是中国最重要的一部经典数学著作,它的完成奠定了中国古代数学发展的基础,在中国数学史上占有极为重要的地位。现传本《九章算术》共收集了246个应用问题和各种问题的解法,分别隶属于方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章。
《九章算术》的产生是社会发展和数学知识长期积累的结果,它汇集了不同时期数学家的劳动成果。三国时的数学家刘徽认为:“周公制礼有九数,九数之流,则《九章》是矣。……汉北平侯张苍、大司农中丞耿寿昌皆以善算命世。苍等因旧文之遗残,各称删补。故校其目则与古或异,而所论多近语也。”根据刘徽的考证结果,《九章算术》源于周公时代的“九数”,而他所见到的《九章算术》是西汉时的张苍、耿寿昌在先秦遗文的基础上删补而成的,其中包括了大量西汉时补充的内容。根据历史文献和出土文物资料来分析,刘徽所言是可信的。《九章算术》所包含的各种算法是汉朝数学家们在秦以前流传下来的数学基础上,适应当时的需要补充修订而成的。按照刘徽的考证,张苍和耿寿昌都是参加过修订工作的主要数学家。《史记•张丞相列传》记载,张苍(约前250~前152)经历了秦、汉两个朝代,他在高帝六年(前201)以攻藏茶有功封为北平侯。“自秦时为柱下史,明天下图书计籍。又善用算律历。”他还“著书18篇,言阴阳律历事。”耿寿昌的生年年代不详,汉宣帝时官至大司农中丞,“以善为算,能商功利”得宠于皇帝(见《汉书•食货志》)。他于天文学主张浑天说,甘露二年(前52)奏“以圆仪度日月行,考验天运状”(见《后汉书•律历志》)。张苍和耿寿昌都是数学名家,又身居高位,由他们主持修订先秦流传下来的《算术》是很自然的事情。根据刘徽的记载,他所注释的《九章算术》最后是由耿寿昌删定的。我们认为耿寿昌删补《九章算术》的年代可以定为这部书完成的年代。

著作影响
《九章算术》是由国家组织力量编纂的一部官方性数学教科书,对两汉时期数学的发展产生了很大的影响。《广韵》卷四有“九章术,汉许商、杜志、吴陈炽、王粲并善之”,《后汉书•马援传》有马续(约70~141)“博观群籍,善九章算术”负记载。此外,史书中还有郑玄(127~200)、刘洪等人“通九章算术”的记述。可知该书是当时学习数学的重要教材,在东汉光和二年(179)一块铜版上的铭文规定:“大司农以戊寅(138?)诏书,……特更为诸州作铜斗、斜、称。依黄钟律历,《九章算术》以均长短、轻重、大小,以齐七政,令海内都同。”这说明该书在东汉时期不仅广为流传,而且度量衡研制涉及的数学问题也要以书中的算法为依据。许商、杜志可能是《九章算书》成书后最早研究过该书的数学家。许商、杜志都是西汉后期的数学家。《汉书•艺文志》著录有《许商算术》26卷、《杜志算术》16卷。这两部书都是汉成帝三年(前26)尹咸校对数术著作之前撰写的。许商、杜志的著作完成年代与耿寿昌删补《九章算术》的年代相去不远,他们的数学著作应当是在研究了《九章算术》的基础上完成的。
《九章算术》不仅在中国数学史上占有重要地位,对世界数学的发展也有着重要的贡献。分数理论及其完整的算法,比例和比例分配算法,面积和体积算法,以及各类应用问题的解法,在书中的方田、粟米、衰分、商功、均输等章已有了相当详备的叙述。而少广、盈不足、方程、勾股等章中的开立方法、盈不足术(双假设法)、正负数概念、线性联立方程组解法、整数勾股弦的一般公式等内容都是世界数学史上的卓越成就。 传本《九章算术》有刘徽注和唐李淳风等的注释。刘徽是中国古代杰出的数学家,他生活在三国时代的魏国。《隋书•律历志》论历代量制引商功章注,说“魏陈留王景元四年(263)刘徽注《九章》。”他的生平不可详考。刘徽的《九章》注不仅在整理古代数学体系和完善古算 理论方面取得了重要成就,而且提出了丰富多彩的创见和发明。刘徽在算术、代数、几何等方面都有杰出的贡献。例如,他用比率理论建立了数与式的统一的理论基础,他应用了出入相补原理和极限方法解决了许多面积和体积问题,建立了独具风格的面积和体积理论。他对《九章》中的许多结论给出了严格的证明,他的一些方法对后世有很大启发,即使对现今数学也有可借鉴之处。
庆祝“圆周率日”别忘了他们 ——刘徽篇
刘徽于三国魏景元四年(公元263年)为 《九章算术》做注,提出用割圆术计算圆周率的方法,计算出正192边形的面积,得到圆周率的近似值为157/50 (即 3.14),在此基础上又计算出正3072边形的面积,得到近似值为3927/1250 (即 3.1416)。刘徽后撰《重差》、《鲁史欹器图》、《九章重差图》,唐代失传。名言:割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣。
在中国,提到圆周率,首先闯入人们脑海的名字无疑是祖冲之,他已经被默认为是中国的“圆周率鼻祖”,就像说仁想到孔子,说木工活想到鲁班一样自然和根深蒂固。但从现存的史料来看,我国古代精确计算圆周率的数学家,应当首推魏晋时期的刘徽,他比祖冲之早入手这个问题两百多年。
提到刘徽,不得不提我国数学史上的一部经典——《九章算术》。后世的数学家,大都是从《九章算术》开始接触、学习、研究并热爱上数学,从此走上了一条跟图形与数字纠缠不清的“不归路”。正是因为《九章算术》无可撼动的经典地位,数学家们争相为其作注,其中最负盛名的当属刘徽所注,称为《九章算术注》。后者虽然是前者的注解,但光芒却在一定程度上覆盖了前者。如同读钱钟书先生的《宋诗选注》,先生评注之精彩喧宾夺主。因为《九章算术注》的空前成功,让人们一时忘却了本应是先入为主的《九章算术》,就好像在婚礼现场,伴娘却比新娘漂亮,搜刮走了宾客们的目光及注意。

现在,让我们回过头来看看《九章算术》,其首章“方田章”就讨论了各种几何图形的度量问题,并且提供了求圆面积的“圆田术”,文中道出了我们今天所通用的方法,即圆面积等于圆周长和半径两者乘积之半。但这里只给出了一个概括性质的方法,或者说,只给了一个目的地,但是如何通往这个目的的路却并没有铺设出来。通俗来讲,就好像是出了一道难题,然后直接写出答案,却并没有给出详细的求证过程。对于一般人来说,知道答案就已经足够,没有兴趣,或者有兴趣也没有能力去勘破这其中奥秘。可刘徽不是一般人,他通过刻苦认真的研究,最终为这篇“圆田术”进行了清晰的注解,后世称为《割圆术》。现代数学家们普遍认为祖冲之计算圆周率的方法就得益于《割圆术》。
《割圆术》全文不过1800余字,却是数学史上一篇不折不扣的千古奇文,这是人类历史上,首次向圆面积极限计算的一次冲锋,同时给出了一个完整的成熟的计算圆周率的高效算法。全篇文章分为三个部分对圆周率的计算进行了翔实的阐述。
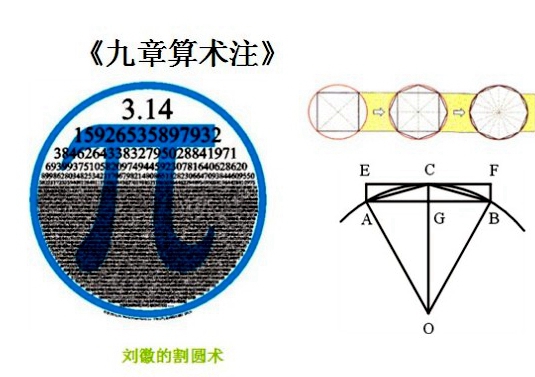
在第一部分,无独有偶,刘徽跟找支点撬地球玩的阿基米德前辈一样想到了内接正边形的方法。刘徽首先从正六边形开始,然后依次乘2分割出内接正12边形、24边形、48边形……刘徽提出了猜想,在无限地扩大之后,终会有一个非常接近圆面积的正边形,求出它的极限值即可获得所求圆的面积,继而得出可接受误差范围之内的π值。
到了第二部分,就是把第一部分的猜想实验之。可以说,第一部分就是绘画了一副施工图,第二部分就是开槽、打地基、搬砖和泥把这个图纸上的二维建筑誊到现实世界。这本应该是一个繁琐耗时的工程,但是刘徽的算法避开了外切多边形,巧妙地节省了计算量,使得他在割到正96边形的时候,就取得了阿基米德曾获得的3.14的精确结果。

到了第三部分,则是在算法实现的基础上进行优化,最大限度地触摸到π的长度。后人证明,如果按照刘徽的计算方法,不断地分割下去,到内接正24576边形时就可以获得祖冲之当时的计算结果,即3.14159265。可是这一切都是借助于现代高度发达的计算机来完成的。在古代只有算筹之类简单,甚至可以说是简陋的运算工具,可想而知,要想完成如此繁重的计算量简直比登天还难。但是刘徽却提供了一种让人拍案叫绝的精加工方法,他将割到192边形的几个浮动的近似值,通过简单的加权平均,获得了具有4位有效数字的圆周率:3.1416。而如果要取得这个值,按照之前的算法则需要切割到3072边形。事实上,越往后面,每一次切割都需要比前一次更加复杂和困难的计算。从192到3072,不仅仅是一个数字的差值,这无疑是一个质的飞跃。即使在一千多年之后的今天,刘徽所提出的优化算法设计的思想深度仍然是矗立在圆周率高精度计算这一领域中一座丰碑,为后人所瞻仰。